GD-77: Ein schöner Einstieg für DMR

FT-817: Strombuchse austauschen

Digitale Signalverarbeitung: ein paar Grundlagen

Irgendwann holen einen die Erinnerungen ein, in diesem Fall beim Lesen der Ausgabe 12/2019 des "Funkamateur" [1]: Vieles erinnerte mich an mein Studium an der Uni Erlangen/Nürnberg. Um 1980 herum brauchten sie am Lehrstuhl für digitale Signalverarbeitung von Hans-Wilhelm Schüßler einen selbst entwickelten Rechner so groß wie eine Waschmaschine, um Sprachsignale mit Telefonqualität verarbeiten zu können. Im Praktikum luden wir die Filterparameter mit einem Lochstreifenleser. So viel, damit der technische Fortschritt auf diesem Gebiet deutlich wird. Bei meinen privaten Basteleien stieg ich damals gerade von Mikroprozessor-Chip SC/MP auf den Z80 um. Typische Taktfrequenz: 4 MHz

Erwin verweist in seinem Artikel auf ein Projekt von I2PHD [2]. Die Dokumentation des Projekts hat mich überzeugt, es mal wieder mit der digitalen Signalverarbeitung die Finger nass zu machen. Wer sich allerdings durch die Dokumentation von I2PHD wühlen will, sollte einige der dort benutzten Konventionen und Techniken kennen. Das Problem gibt es sicher nicht nur da. Dieser Artikel soll die Voraussetzungen schaffen, um solche Texte grundsätzlich verstehen zu können. Es geht mir nicht um eine komplette Einführung in das Gebiet.

Viele haben schrecklich Angst vor Formeln. Dabei ist das in vielen Fällen völlig überflüssig: Ingenieure benutzen Formeln gerne als Kurzschrift, um Zusammenhänge kurz und eindeutig darzustellen. Niemand hat vor, mit diesen Formeln höhere Mathematik zu betreiben: Ingenieure nutzen Mathematik als Handwerkszeug, aber wollen damit nichts beweisen. Richtig ist die Problemlösung, die am Ende herauskommt: ein Produkt. Mathematiker halten uns deshalb für Banausen – sollen sie doch.

Jetzt aber zu der Terminologie, die im Zusammenhang mit digitaler Signalverarbeitung regelmäßig auftaucht:

• z^-1 bedeutet schlicht die Verzögerung um einen Verarbeitungstakt. Wenn dann in einer Formel z^-5 auftaucht, wird das Signal von 5 Takten später (also weiter vorne in der Verzögerungskette) mit einem bestimmten Faktor multipliziert und zum Signal addiert.

Digitale Signalverarbeitung funktioniert in weiten Grenzen so, dass man das Eingangssignal durch eine lange Kette von Speicherzellen schiebt – alle Abtastwerte im Gänsemarsch durch beispielsweise 1000 Speicherzellen. Von den Ausgängen der Speicherzellen werden die Abtastwerte an Rechenwerke weitergegeben, die erst mal multiplizieren und dann diverse Signale aufaddieren. Das Rechenergebnis wird mit dem nächsten Takt in die nächste Speicherzelle übernommen.

Daraus, welche früheren oder späteren Abtastwerte mit welchen Verstärkungsfaktoren jeweils kombiniert werden, ergibt die gewünschte Funktion. Beim Bestimmen dieser Verknüpfungen wird wirklich höhere Mathematik benötigt. Aber dafür gibt es genug Kochrezepte, beispielsweise in Form fertiger Programmcodes. Wer ein analoges Filter mit Hilfe eines einschlägigen Programms dimensioniert, macht nichts anderes.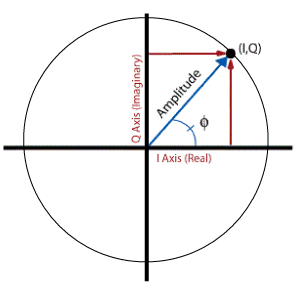

• Die parallele Verarbeitung von Sinus und Cosinus lässt sich am Einheitskreis nachvollziehen. War da mal was mit Trigonometrie? In der Ingenieurmathematik hat eine Potenz mit einem negativen Exponenten regelmäßig was mit dem Einheitskreis zu tun: (-1)² = (-1) * (-1) = 1, was der Radius des Einheitskreises ist. Umgekehrter Schritt: Die komplexe Einheit j ist definiert als die Quadratwurzel aus -1. z^-1 kann man also lesen als einmal um den Einheitskreis rum – also eine Taktperiode lang.
• Φ (großes Phi) bedeutet Winkel. Ein z^-1 und ein Φ bedeutet also, den Zeiger im Einheitskreis pro Taktperiode um den Winkel Φ weiter zu drehen.

Bei einer festen Taktfrequenz kann man mit dem Ändern von Φ also die Frequenz eines Oszillators bestimmen. Bei Φ = 90° ist die Oszillatorfrequenz ein Viertel der Taktfrequenz. In dem Fall ergibt sich der Cosinus zu einem bestimmten Zeitpunkt als Sinus des Zeitpunktes vorher und der Sinus als der -Cosinus des Zeitpunktes vorher.

Ganz grundsätzlich gilt, dass immer die um 90° verschobenen I- und Q-Komponenten eines Signals gemeinsam betrachtet werden.

• Die Kombination von zwei, um 90° verschobenen Komponenten eines Signals wird als komplexes Signal bezeichnet.

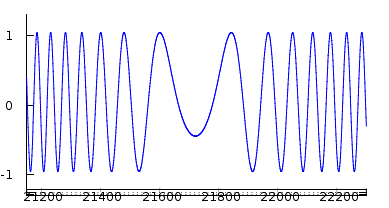
Deshalb beginnt digitale Signalverarbeitung fast immer mit zwei Mischern, deren Oszillatorsignale um 90° gegeneinander verschoben sind. Im Prinzip kann man das auch analog machen, wie das QRP-Labs beim CW-Transceiver QCX [3] macht, um bei einem Direktmischer das ungewünschte Seitenband zu unterdrücken. Analogtechnik hat Probleme wie Bauteiltoleranzen und nicht-ideales Verhalten der Elektronik. Beim QCX funktioniert das nur deshalb so gut, weil der CW-Empfänger eine so geringe NF-Bandbreite hat. Trotzdem hat der Phasenschieber drei Abgleichpunkte.

Ehe jetzt jemand am Schaltbild des QCX verzweifelt sucht: Beim Nulldurchgang eines Signals am Mischer kennen wir das Verhalten, dass die Differenzfrequenz immer niedriger wird und dann wieder höher. Was man dabei aber nicht bemerkt, ist der Phasensprung um 180° beim Nulldurchgang. Anders ausgedrückt: Der Zeiger im Einheitskreis dreht sich plötzlich in die entgegengesetzte Richtung. Das sieht man erst dann, wenn man beide Komponenten des komplexen Signals gemeinsam betrachtet.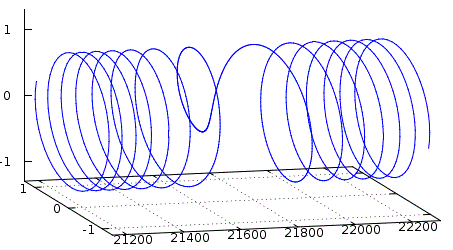

Aus den beiden Mischern kommt das gleiche Signal raus, aber eben um die 90° der Oszillatorsignale verschoben. Die folgenden Operationsverstärker sind als Allpässe beschaltet. Sie ändern nichts an der Amplitude des Signals, aber verzögern es frequenzabhängig: Ein 1-kHz-Signal wird um 250 µs verzögert, ein 500-Hz-Signal um 500 µs – an einem Sinus-Signal sieht man, dass das jeweils 90° sind.

Diese Verschiebung läuft jetzt für beide Seitenbänder in die gleiche Richtung. Addiert oder subtrahiert man die beiden Signale, löscht sich jeweils das ungewünschte Seitenband aus. Genau an dieser Subtraktion scheitern analoge Lösungen, sobald die Signale breitbandig werden. Digital kann man hier aber beliebig genau rechnen.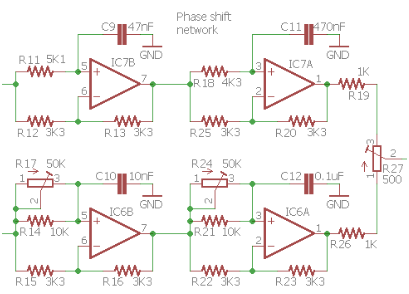

Digital kann man zwar beliebig genau rechnen, aber doch nicht völlig exakt; überall gibt es Rundungsfehler. Das gilt sowohl für die Abtastwerte, als auch für die Koeffizienten, mit denen die Signale multipliziert werden. Dazu kommt, dass beim Multiplizieren und Addieren häufig sehr große Zahlen entstehen. Überläufe lassen sich in den Rechenwerken häufig nur dadurch vermeiden, dass man Nachkommastellen wegwirft. Also entstehen auch hier Verzerrungen, die aber um viele Größenordnungen geringer sind als bei der Analogtechnik.

Beim Filtern schaltet man, wie schon oben erwähnt, lange Verzögerungsketten zusammen. Dabei benutzt man gerne FIR-Filter [4], weil die nicht ins Schwingengeraten können:

• FIR ist die Abkürzung für finite impulse response. Das bezeichnet eine Klasse von Filtern, bei der es eine (meist größere) Zahl von verketteten Verzögerungsblöcken gibt, es innerhalb des Filters aber keine Rückkopplungen gibt. Anders ausgedrückt: Der Ausgang eines Verzögerungsblocks ergibt sich ausschließlich als Werten, die in vorherigen Stufen bestimmt wurden. Beispiel: 1000 Verzögerungsblöcke hintereinander und 1 MHz Taktfrequenz bedeutet bei einem FIR-Filter, dass ein beliebiges Eingangssignal sich nach 1 ms nicht mehr auf das Ausgangssignal auswirken kann.

Sorry, ich weiß: Obiges erschließt sich frühestens beim dritten sorgfältigen Lesen. Das ist aber die Quintessenz aus einem Studienschwerpunkt bei einem Pionier dieses Gebiets über mehrere Semester hinweg.

Literatur

[1] Serlé, Erwin (PE3ES): SDR-Experimente auf LW und MW mit dem STM32F429 Discovery

In: Funkamateur 12/2019, S. 1158f

[2]di Bene, Alberto (I2PHD): ARM Radio : a project for the ARM MCU Design Contest

https://www.i2phd.org/armradio/index.html

[3] QRP-Labs: CW-Transceiver QCX

[4] Ossmann, Martin: Entwurf von FIR-Filtern, nicht nur für den Red Pitaya

In: Funkamateur 4/2018, S. 336ff

[5] Kuisma, Mikael Q.: I/Q Data for Dummies

Aus dieser Website stammen die Bilder auf dieser Seite. Herzlichen Dank an Mikael, dass er diese Bilder allgemein zur Verfügung stellt.